

The Gaussian elimination rules are the same as the rules for the three elementary row operations, in other words, you can algebraically operate on the rows of a matrix in the next three ways (or combination of): This last step will produce a reduced echelon form of the matrix which in turn provides the general solution to the system of linear equations. If is possible to obtain solutions for the variables involved in the linear system, then the Gaussian elimination with back substitution stage is carried through. If found that the system has no solution, then there is no reason to continue row reducing the matrix through the next stage. Such stage has the purpose to demonstrate if the system of equations portrayed in the matrix have a unique possible solution, infinitely many solutions or just no solution at all. The forward elimination step refers to the row reduction needed to simplify the matrix in question into its echelon form. These two Gaussian elimination method steps are differentiated not by the operations you can use through them, but by the result they produce. This technique is also called row reduction and it consists of two stages: Forward elimination and back substitution. Gaussian elimination is the name of the method we use to perform the three types of matrix row operations on an augmented matrix coming from a linear system of equations in order to find the solutions for such system.
#Lesson 3 . 7 variable linear equation systems page 50 how to
If we multiply both sides of the first equation by -3, then we will be able to eliminate the x -variable.Solving a linear system with matrices using Gaussian eliminationĪfter a few lessons in which we have repeatedly mentioned that we are covering the basics needed to later learn how to solve systems of linear equations, the time has come for our lesson to focus on the full methodology to follow in order to find the solutions for such systems. In this case, let’s focus on eliminating x. With the addition method, we want to eliminate one of the variables by adding the equations.
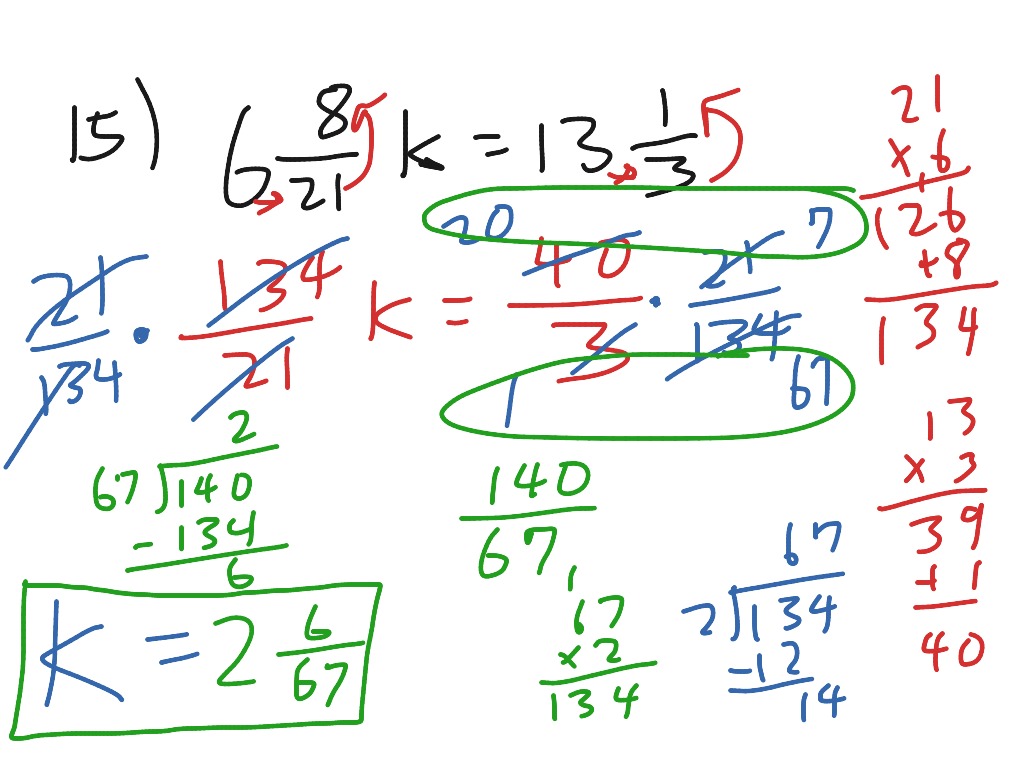
The graphs of the equations in this example are shown below. Parallel lines will never intersect thus, the two lines have no points in common. Writing the equations in slope-intercept form confirms that the system is inconsistent because all lines will intersect eventually unless they are parallel. For example, consider the following system of linear equations in two variables. In this section, we will look at systems of linear equations in two variables, which consist of two equations that contain two different variables. Even so, this does not guarantee a unique solution. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Some linear systems may not have a solution and others may have an infinite number of solutions. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously.

In order to investigate situations such as that of the skateboard manufacturer, we need to recognize that we are dealing with more than one variable and likely more than one equation. (credit: Thomas Sørenes) Introduction to Solutions of Systems


 0 kommentar(er)
0 kommentar(er)
